Inside a dielectric, the time independent Maxwell curl equations with a positive time convention ( ejωt ) are
![]()
and the divergence equations are
![]()
In the magnetic formulation, the electric field is eliminated from (1) by taking the curl
of the second equation and substituting from the first. For regions of constant permittivity ε , there are no gradients of ε , and the equation simplifies to
![]()
In view of the vector identity ∇×∇×A = ∇( ∇ ⋅ A ) – ∇2 A , and the property of H having zero divergence, (3) becomes
![]()
where ![]() is the free space wavenumber.
is the free space wavenumber.
It is true that it is usually the electric field, and not the magnetic field, that is of interest for applications. The motivation for solving the problem with a magnetic formulation is that the waveguide structure is created by introducing discontinuities in electric permittivity,
ε, and not magnetic permeability, μ . When matching boundary conditions at layer boundaries, the normal component of the electric field is discontinuous, since it is the electric displacement, D= εε0 E , and not the electric field that is to be made continuous. Since the permeability is the vacuum level μ0 everywhere, all components of the magnetic field are continuous at all boundaries. The finite difference representation of continuous functions is more accurate than discontinuous functions, and therefore a finite difference formulation based on the magnetic field gives more accurate results than one based on electric fields.
The electric fields are still needed for applications. These fields can be calculated after the fact by taking the curl of the magnetic field (using the second equation in (1)) by finite differences. Explicitly,
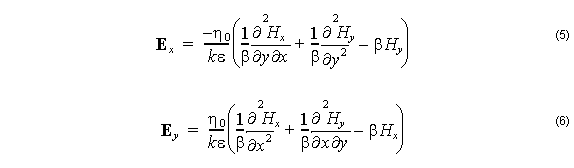
In the mode solving problem, the permittivity ε does not vary with z, and so the solution for the magnetic field can be expected to be an harmonic function of z:
![]()
and (7) in (4) gives
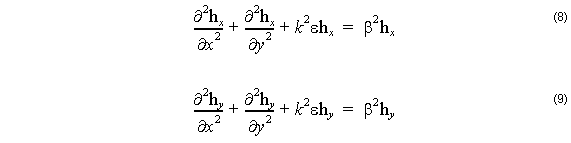
Since the β is unknown, the mode solving problem is really an eigenvector problem with β2 as the eigenvalue, and the function hx ( x, y ) or hy ( x, y ) as the eigenfunction.

