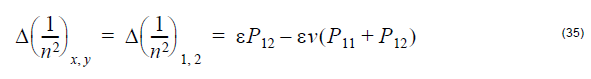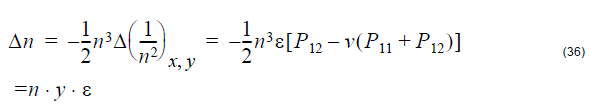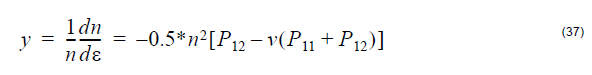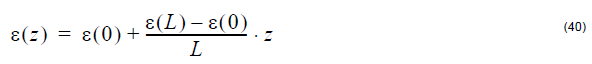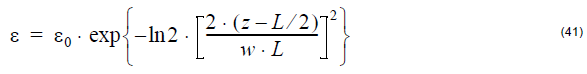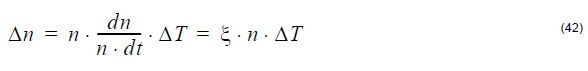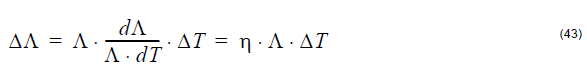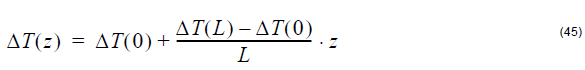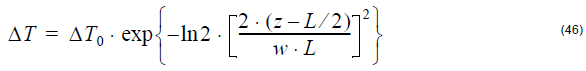Temperature and strain change the grating period as well as the grating refractive
index. Consequently, the response of the grating device is changed when
temperature and strain distributions change.
Strain-optic effect of fiber Bragg grating
The changes of optical indicatrix caused by strain are:
where, ε1 = ε2 = –vε, ε3 = ε, ε4 = ε5 = ε6 = 0 (no shear strain), and ε
being the axial strain in the optical fiber. The symbol v denotes the Poisson’s ratio
for the fiber.
The strain-optical tensor for a homogeneous isotropic material is:
where Pij are the strain-optic constants,
The refractive index change is:
where the strain-optic coefficient y is defined as:
The grating period changes is:
The default strain distributions that can be applied to a fiber grating are listed below:
- Uniform
where ε0 is the constant strain.
- Linear
where L is the grating length, ε(0) is the strain at z = 0, and ε(L) is the strain
at z =L
- Gaussian
where ε0 is the peak strain value and w is the normalized value of FWHM.
Other strain distributions can be defined by user functions.
Thermal-optic effect of fiber Bragg grating
The temperature-induced refractive index change is:
where ξ is the thermo-optic coefficient of the fiber and ΔT is the temperature
change.
The temperature-induced grating period change is:
where η is the thermo-optic expansion coefficient.
The default temperature distributions that can be applied to a fiber are listed below:
- Uniform
where ΔT0 is the constant temperature.
- Linear
where L is the grating length, ΔT(0) is the temperature at Z = 0, and ΔT(L) is
the temperature at z = L.
- Gaussian
where ΔT0 is the peak temperature value and w is the normalized value of FWHM.
Other temperature distributions can be defined by user functions.