[Luis RodriguezParticipant]

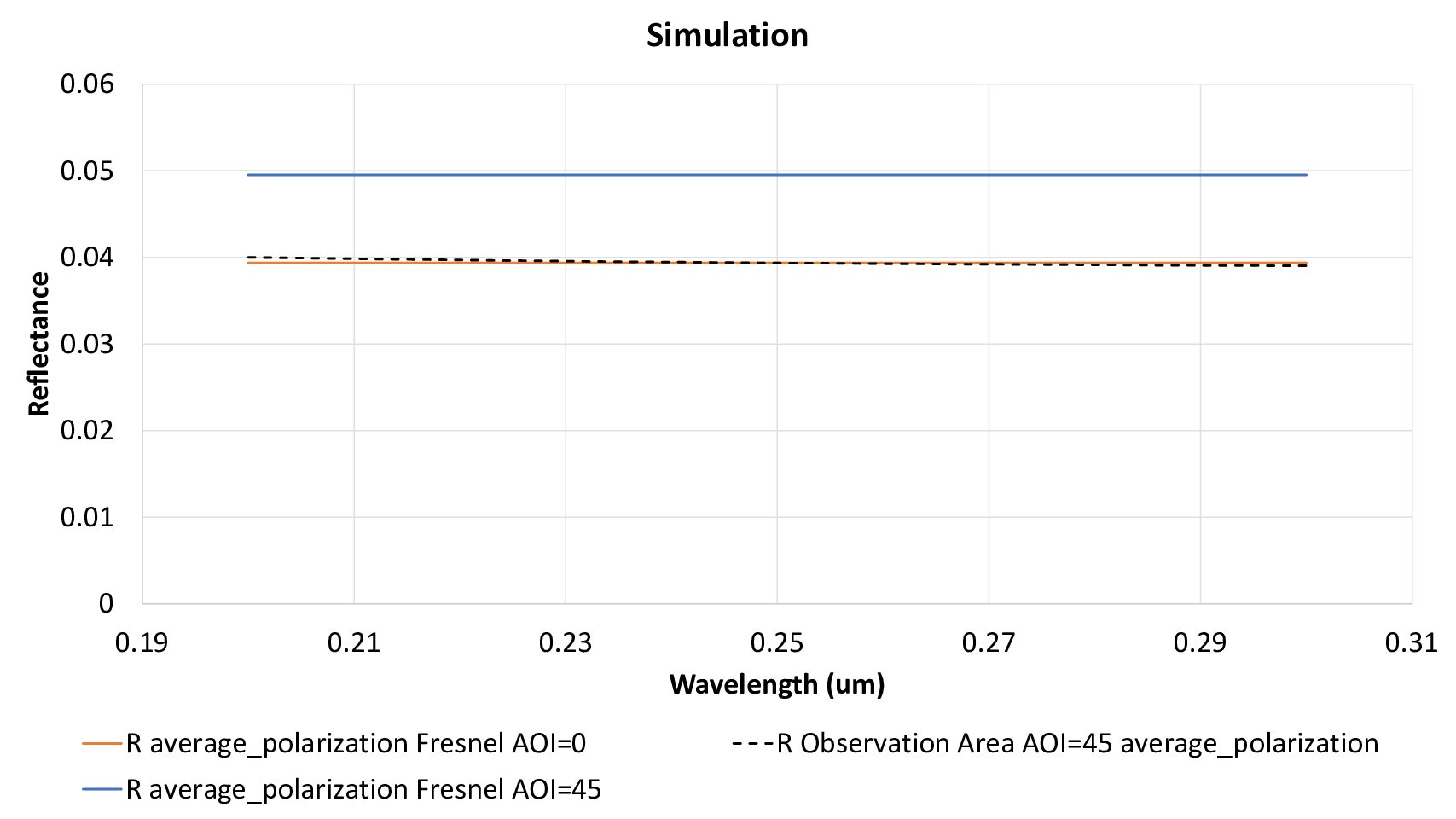
And this is the result of the simulation using a tilted wave at 45degrees compared with what you obtain using Fresnel equations. All reflectances are averaged for both polarizations.

Attachments:

1. 

   Problems-OptiFDTD-Tilted-Wave.pdf
   

[Luis RodriguezParticipant]

Hi Scott,

Thanks for your feedback! I am using the 32-bits free version.

Regarding your answer, the point is that the nano structures are smaller than the wavelength, so there should not be any divergence or convergence. Indeed, looking at Ez in the reflected field, I see that is close to 0 across the spectrum, meaning that there is not diffraction due to the nano structures.

I tried to move both observation area and observation points further to meet the far field approximation and still results are very different at the target wavelength. I am clueless 🙂

Thanks,
Luis

[Luis RodriguezParticipant]

Some additional information: I have attached the design file, and in the attached picture you can see the differences between the reflectivity calculated from an observation area and from an observation point. I am only interested on specular reflectivity

Regarding R from the observation area, I used the power spectrum option and then I calculated Pz normalized to input plane.

Regarding R from the observation point, I calculated the normalized DFT for Ex, Ey, and Ez and then R=(Ex)^2+(Ey)^2+(Ez)^2

Overall the coincidence is acceptable, but the ball should enhance the reflectivity at 0.0165 microns, and it only happens when I calculate R from the observation point. However, when I use the observation area, results are different.

I am lost! Any help would be very welcome!

Attachments:

1. Observation-Area-vs-Point-pdf.pdf
2. SatellitePeakEUV.fdt