In this lesson we check that the layer peeling algorithm can reconstruct an unknown
grating with knowledge of only the reflection coefficient. In the first step, we select a
typical grating with chirp and apodization and calculate its reflection coefficient. This
spectrum is then exported to a text file. In the next step, OptiGrating is run again and
the spectrum file imported. The layer peeling algorithm is applied to the imported
spectrum to reconstruct the original grating.
| Step | |
| 1 | File > Open. Choose file Ex1a.ifo. |
| 2 | Select the Profile tab to see the details of this grating.
|
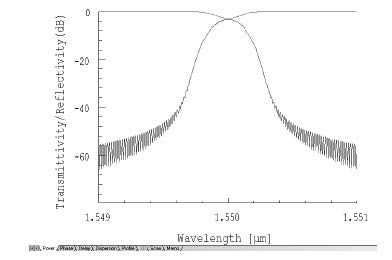
| 3 | Select the Power tab to see the reflection and transmission spectra.
Note: You can press Calculate to calculate the spectrum again, if desired. |
| 4 | Click on Spectrum in the Single Fiber drop down menu, then click on the graph in the main window to active it. |
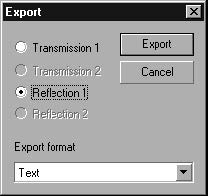
| 5 | Select Tools > Export Complex Spectrum and select the Reflection button as shown below: |
| 6 | Click Export. |
| 7 | In the Save As dialog box, find a suitable place and name for your data file. |
| 8 | Close Ex1a.ifo. |
| Step | |
| 1 | Now, open a new project with File > New > Single Fiber. |
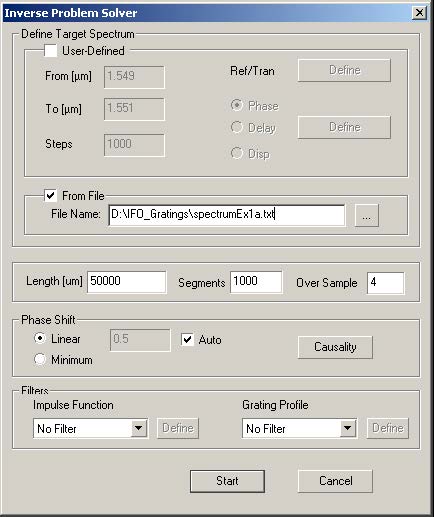
| 2 | Choose Calculation > Inverse Scattering Solver to get the Inverse Problem Solver dialog box. |
| 3 | Select the From File checkbox. |
| 4 | Navigate to the place where you left the file with the reflection spectrum. Open the file. |
| 5 | We suppose that the original length of the grating is known, so enter 50000 μm in the Length box. (Feel free to experiment with different lengths.)
|
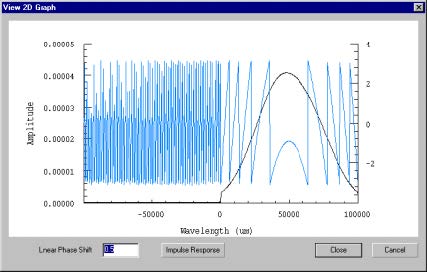
| 6 | Click on the Causality button to test this spectrum.
|
| 7 | Click Close. |
| 8 | Click Start in the Inverse Problem Solver dialog box to begin the reconstruction. |
| 9 | Click on Spectrum to enable all tabs. |
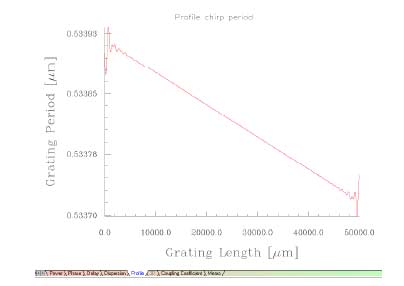
| 10 | Select the Profile tab to see the reconstructed profile.
|
| 11 | To see the chirp more clearly, right click the mouse in the Profile window and select Chirp Period.
. . . to get the following:
|
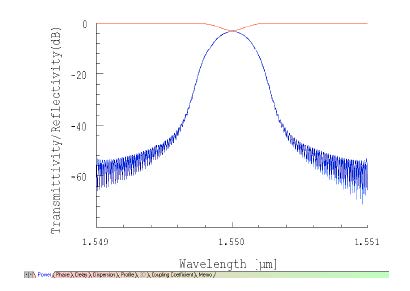
| 12 | Select the Power tab to compare the reflectivities, one from the imported complex spectrum and the other from the calculated response of the reconstructed grating. |